1 Predicates

1. The following are equivalent to p ⇐⇒ q? True or False.

(a) (¬p ∨ q) ∧ (q → p)

(b) (¬p ∧ q) ∨ (p ∧¬q)

2. Fill in the truth table for each of ¬p,¬q,p∨q,p∧q,p → q,q → p,¬q →¬p

p q ¬p ¬q p ∨ q p ∧ q p → q q → p ¬q →¬p

T T

T F

F T

F F

3. Let x − y = z be denoted by Q(x, y, z), over the set -of integers. Find these truth values:

Q(4, -3, 7) =

Q(1, 3, 4) = Q(x, 3, z) =

2 Propositions

4. How to denote the Translation from English to Logic

“ All students in this class have visited Uluru ”

S(X) = ”X is a Student in this Class C(Y) = ”Y has visited Uluru”

5. If P(x) denotes x < 3, find these truth values:

• P(3) ∨ P(−2)

• P(5) ∧ P(−1)

• P(6) → P(−1)

• P(2) →¬P(−1)

6. Write in logical format the requirements for a function:

Function Fix (a, b) which only accepts a > b, a > 0 and which outputs all integers from b to a.

3 Proofs

7. Let A and B be sets. Show that A + B - C = (A - C) + (B - C)

8. Prove that m2− n2 = 0 ⇐⇒ (m = −n) ∨ (m = n)

9. Let m be a positive integer. Prove that

a ≡ b (mod m) ⇐⇒ (a (mod m) = b (mod m).

4 Matrices and circuits

10. Find the product A.B where

12. Draw a logic circuit for this proposition: (p ∧ q) ∨ r

What is the output if p =1, q=1 r=0

5 Pseudo code

13. Describe an algorithm in pseudo code (i.e. structured english) for finding the difference of two binary expansions

14. Describe an algorithm in pseudo code for calculating: 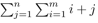 for given parameters n and m

15. How do you add a word to a dictionary stored in a Trie structure.

Describe in pseudo code or code how to do this.

6 Advanced proofs

16. Prove or disprove that : ∀m,n ∈Z: if (2m + n) is odd then m and n are both odd.

17. Prove or disprove: The difference of the squares of any two consecutive integers is odd. (Note: ∀n,m ∈Z n,m are consecutive ⇐⇒ m=n+1.) Full marks for proof, not just example.

18. Prove that ¬(p ∨ (¬p ∧ q)) is equivalent to ¬p ∧¬q Full marks for proof, not just example.

1. ¬(p ∨ (¬p ∧ q)) = given

7 Advanced

19. Which of the following sets of numbers are closed under:

(a) addition

(b) multiplication

(c) subtraction

(d) division

Provide proof of each statement.