Question: Run step 5 “Identify the resonant frequencies in a building model” in the file under the name of “multipleMassSpringDamper.mlx” and record the results in a word file based on the given instructions.

Solution procedure:

1. Understand the problem statement.

2. Identify the resonant frequencies of the mass-spring-damper building model as shown in the below figure and follow the given instructions.

a) Open the Simulink model msdMultipleBuilding.slx, which models a building with 20 floors.

b) This model has 20 degrees of freedom, so the constant vectors and initial values of the system must be constructed to match. Run this section to populate the parameters. Note that the building is given an initial offset in the initial condition x_dot_0.

c) Set the Index in the Selector block to 20 so that the spectrum is measured for x20, the displacement of the 20th floor. Set the forcing magnitude (F0) to zero and the simulation stop time to 200.

d) Run the model and use the peak finder tool in the Spectrum Analyzer block to identify the prominent frequencies. Record the period of oscillation for the two most prominent peaks. Recall that the period T = 1/f, where f is the frequency.

e) Create a table in a word file to record the period of oscillation for the two most prominent peaks below:

f) Save the plots from the Scope (Time domain) and from the Spectral Analysis (Frequency domain) and past them in the previous word file without any description and then save the word file.

3. Set the initial conditions to zero by running this section (code lines 46 and 47) and answer the bellow question in the same word file that you created in the previous step:

a) The model contains a subsystem (F1) that produces a periodic forcing 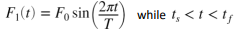 and 0 otherwise. The forces on the other masses are zero. Set the period, T, of the forcing to the strongest resonant period and the amplitude (F0) to F0 = 1 and observe if there is a resonant response. 

b) Try setting the periodicity of the forcing to T = 1.5 s. Is the response reduced?

c) Try setting the periodicity of the forcing to the second natural period that you measured. Is there a resonant response?

Dataset