Q 10. Let T be the following deterministic Turing machine with input alphabet Σ = {0, 1} and tape alphabet Γ = {0, 1, 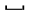
(a) Show how this machine processes the words 10 and 001.
(b) What string will be written on the tape after T processes an input of 101010?
(c) Briefly describe in words what T does. Does T run in polynomial
time? If so, give the smallest k ∈ N such that t(n) ∈ O(n
k
). Justify your answers.
Students succeed in their courses by connecting and communicating with an expert until they receive help on their questions

Consult our trusted tutors.