QUESTION 1

a) Name four goals of an econometric analysis.

b) Differentiate between simple regression and multiple regression models. Give one example each.

c) Describe two (2) types of economic data sets.

d) A firm applies the model 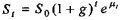 for sales volume prediction

where:

st - sales in year t

g - the growth rate of sales

t - number of years

i) Obtain an appropriate equation if OLS technique is applied.

ii) Compute the growth rate (g) if S0 and ln(i + g)are 3.671 and 0.059 respectively.

iii) Estimate the firm's sales for the next 5 years.

e) Interpret the slope coefficient for the following functional forms.

QUESTION 2

Consider the following estimation results using Cobb-Douglas production function for the period 1985-2004.

where Y is gross domestic product (GDP), and L and K are labour and capital inputs respectively.

a) Perform t-test for each variable at 5% level of significance.

b) Interpret the coefficients of In Lt and In Kt.

c) How would the significance of estimated R2 be tested at 5%?

d) How well does the model explain GDP?

e) If the production function exhibits constant returns to scale, derive the new equation that can be estimated algebraically.

f) As an alternative, the following specification is estimated:

By comparing both models ([2a] and [2b]) in terms of coefficient of determination, can we conclude that model [2a] is better than model [2b]? Why or why not?

QUESTION 3

a) "The existence of serial correlation is due to violation of one of the classical assumptions". Explain.

b) The scatter diagram below shows the residual plot from a regression model.

i) Describe the relationship between residuals ut and Mu-1.

ii) Suggest the order of serial correlation.

iii) How can such a relationship be formally detected?

c) Based on 85 observations, the estimation results of demand for electricity are given as:

i) What are the expected signs of the coefficients of this model?

ii) Are the empirical results in accordance with prior expectations?

iii) Detect the existence of serial correlation at 5% level of significance.

QUESTION 4

a) What is meant by 'dummy variable'?

b) Consider the following basic model:

where Y = annual salary of a university professor

X = years of teaching experience

D = dummy for gender (1=male and 0=female)

Derive and draw the regression equation if:

i) there is a difference in intercepts between male and female.

ii) there is a difference in slopes but having the same intercept.

iii) the slopes and intercepts are different

c) In an effort to examine the saving behaviour among households in Peninsular Malaysia, the following regression models were estimated based on 8,000 households. The dependent variable is average household's savings s, and the independent variables are average household's income x, and dummy variable D, (1-rural region and 0-urban region). The figures in parentheses are the estimated standard errors.

 i) Write down the estimated equation for both models.

ii) How do you know that "region" plays an important role in determining average household savings?

iii) Compute the marginal propensity to save for rural and urban households.

QUESTION 5

a) Differentiate between perfect and imperfect multicollinearity.

b) With 50 observations, the wage rate regression model was estimated as follows:

i) Is there multicollinearity in the above regression equation? How do you know?

ii) Compute variance inflation factor (VIF) if the correlation coefficient between Ht and Lt is 0.987.

 iii) Based on answer in (ii), what is your conclusion?

iv) Suppose that the relationship between Ht and Lt is given by: 

Ht =24-Lt

and the general form of wage rate regression model is:

Derive the new regression equation in order to solve multicollinearity.

c) i) Describe two (2) consequences if heteroscedasticity is present.

ii) Discuss how to detect heteroscedasticity using Park Test.