T test

---

• Assumptions

• ·        One sample t test is used when sample size is small (<= 30) or population standard deviation is unknown.
• ·        Method of simple random sampling is used
• ·        Data is normally distributed

• 5 Step Hypothesis

Hypothesis

Ho: population mean is equal to μo. μ = μo

Ha1: population mean is equal to μo. μ≠μo  (Two tailed test)

Ha2: population mean is equal to μo. μ<μo  (Left tailed test)

Ha3: population mean is equal to μo. μ>μo  (Right tailed test)

Here μo takes a particular value.

 Test Statistic

 Critical value

-t(a/2,n-1),t(a/2,n-1) (Two tailed test)

-t(a,n-1) (Left tailed test)

t(a,n-1) (Right tailed test)

P-value

2*(1-P(T≤|t|)  (Two tailed test)

P(T≤t)  (Left tailed test)

P(T≥t)  (Right tailed test)

 Decision rule

Reject Ho if |t| > t(a/2, df) or p-value < alpha (two tailed test)

Reject Ho if –t < -t(a, df) or p-value < alpha (left tailed test)

Reject Ho if t > t(a, df) or p-value < alpha (right tailed test)

• Confidence Interval

Standard error (SE) and margin of error (ME) is given by:

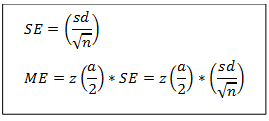
 100(1-alpha)% Confidence interval for population mean is given by:

This implies I am 100(1-alpha)% confident that estimated population mean lies in the obtained interval.

One sample t test CALCULATOR