Q3) A belief network shown below (Figure 2) describes the relation between four variables A, B, C, and D, along with their conditional probability tables (CPT). Each variable takes different states as given below.

A ∈ {0, 1}

B ∈ {0, 1}

C ∈ {0, 1, 2}

D ∈ {0, 1, 2} 

3.1) Obtain an expression (in a simplified form) for

P(C = 1| A = 1, B = 0, D = 2) (Show the steps clearly).

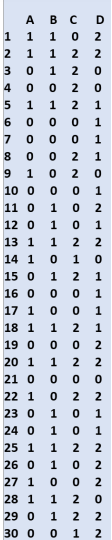
3.2) The table shown below provides 30 simulated data obtained for the above Bayesian network. Use this data to find the maximum likelihood estimates of α, β, λ and σ.

3.3) Find the value of P(C = 1 | A = 1, B = 0, D = 2) using the appropriate values obtained from the above question Q3.2.

3.4) Now consider the following values for α, β, λ and σ, to answer the following question: a = 0. 3 , β = 0. 4, λ = 0. 5, σ = 0. 3.

Use the below libraries in R to create the above belief network along with the probability values using R-programming, as shown in the CPT tables of Figure 2.

You may use the following libraries for this:

#https://www.bioconductor.org/install/

#BiocManager::install(c("gRain", "RBGL", "gRbase"))

#BiocManager::install(c("Rgraphviz"))

library("Rgraphviz")

library(RBGL)

library(gRbase)

library(gRain)

#define the appropriate network and use the “compileCPT()”function to Compile list of conditional probability tables, and create the network.

a) Write R code and show the obtained belief network for this distribution.

b) Show the probability tables obtained from the R output, (and verify with the above table).

c) Use R program to compute the following probabilities:

i) Find the joint distribution of B, C and D.

ii) Find the marginal distribution of C.

iii) Find P(A=0 | C=2, D=1).