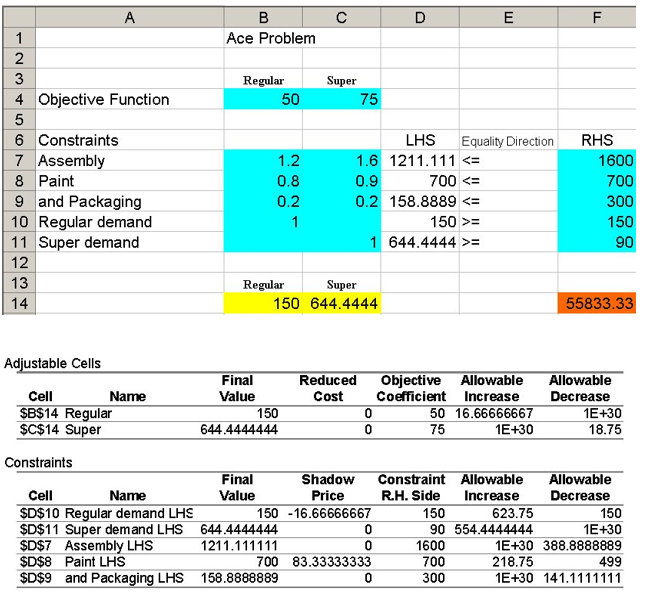
5.  The Ace Manufacturing Company produces two lines of its product, the super and the regular.  Resource requirements for production are given in the Table below.  There are 1,600 hours of assembly worker hours available per week, 700 hours of paint time, and 300 hours of inspection time.  Regular customers will demand at least 150 units of regular line and 90 of the super.

The linear programming formulation for this product mix problem is:

Decision variables

x1 = units of regular produced

x2 = units of super produced

Formulation

Maximize Z = 50x1 + 75x2

s.t.

1.2x1 + 1.6x2 ≤ 1600   Assembly time

  .8x1 +   .9x2 ≤   700   Paint time

  .2x1 +   .2x2 ≤   300   Inspection time

     x1              ≥    150  Regular demand

                  x2 ≥      90  Super demand

      x1, x2  ≥ 0

Answer the following questions on this page and the next page referring to the above formulation and the printout on the page following the questions

a.   What is the optimal solution (complete answer!)?

b.  If demand for regular increased by 10, what will happen to the optimal solution (Z and decision variables)?

c.  If demand for super increased by 10, what will happen to the optimal solution (Z and decision variables)?

d. If the profit contribution of regular decreased to 30, what will happen to the optimal solution (Z and decision variables)?

e.  If the profit contribution of super decreased to 55, what will happen to the optimal solution (Z and decision variables)?