5. Histogram methods

Consider a dataset {xj} n j=1 where each point x ∈ [0, 1]d . Let f(x) be the true unknown data distribution. You decide to use a histogram method to estimate the density f(x) and divide each dimension into m bins.

(a) Show that for a measurable set S, E[1{x∈S} ] = P(x ∈ S).

(b) Combining the result of the previous question with the Law of Large Numbers, show that the estimated probability of falling in bin i, as given by the histogram method, tends to 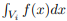, the true probability of falling in bin i, as n → ∞. Vi denotes the volume occupied by bin i.

(c) Consider the MNIST dataset with 784 dimensions. We divide each dimension into 2 bins. How many digits (base 10) does the total number of bins have?

(d) Assume the existence of an idealized MNIST classifier based on a histogram of m = 2 bins per dimension. The accuracy of the classifier increases by ε = 5% (starting from 10% and up to a maximum of 100%) each time k = 4 new data points are added to every bin. What is the smallest number of samples the classifier requires to reach an accuracy of 90%?

(e) Assuming a uniform distribution over all bins, what is the probability that a particular bin is empty, as a function of d, m and n?

Note the contrast between (b) and (e): even if for infinitely many datapoints, the histogram will be arbitrarily accurate at estimating the true distribution (b), in practice the number of samples required to even get a single datapoint in every region grows exponentially with d.